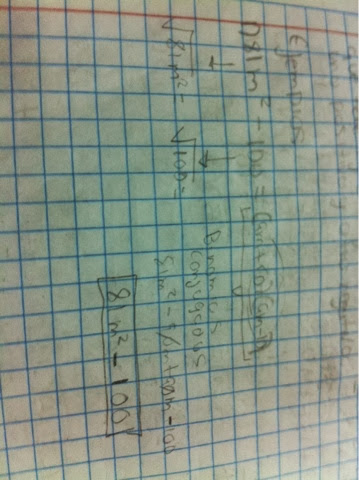Expresiones cuadraticas por medio de factorízacion

Pues esto caso se resuelve. Con todos los casos anteriores identificando cual utilizar .

Cuarto caso de factorízacion “diferencia de cuadrados”

Al factorízar una diferencia de cuadrados se obtiene trinomios conjugados los cuales son aquellos que tienen un término común y 2 términos simétricos . 

Para factorízar este tipo de expresiones se hace lo sig. 

1. Se extrae la raíz de ambos términos , el término positivo es el que dará de resultado en término común 

2. Al extraer la raíz cuadrada del término que tiene signo negativo se obtendrá 2 resultados un positivo y otro negativo .

Tercer caso de factorízacion “trinomio de segundo grado”

Los casos a seguir para factorízar este tipo de trinomios:

1.sacar la raíz cuadrada del término cuadratico

2.buscar 2 números que sumados algebraicamente nos den el coeficiente del término lineal

3. Y estos mismos números pero multiplicados nos den el término independiente.

Segundo caso de factorízacion

Trinomio cuadrado perfecto.

Para factorízacion el trinomio cuadrado perfecto se necesita cumplí las sig. condiciones :

1.la expresión algebraica tiene que tener 3 términos

2.2 términos tienen que tener raíz cuadrada perfecta 

3. Al sacar las 2 raíces y multiplicarlas por 2  Debe dar el término no utilizado 

Con esto se cumple que es un trinomio cuadrado perfecto 

Y para factorízar se toman las  2 raíces  obtenidas separadas por un signo del término que no se le sacó raíz 

Al factorízar un trinomio cuadrado perfecto. Se obtiene  un binomio al cuadrado.

Primer caso de factorízacion.

Para resolver este método se hace estos pasos

1. Determinar el máximo común divisor de todos los números 

2. Determinar el factor común en los literales , tomar la letra que se encuentre en todos lo términos  con menor exponente 

3.dividir cada factor entre el factor común y así se obtendría el segundo factor 

4 si los factores solo constan de una solo incógnita se resuelven como una ecuación normal 

5. Se realiza las comprobaciones con la ecuación original 

Ecuaciones cuadraticas

 Ecuaciones cuadraticas 

Forma general : ax2 + bx + c = 0

Completa:                      Incompleta 

                                   Ax2 + bx =0

                                   X2 - 81=0

 

X2 + 8x + 16 =0

Solución por factorízacion :

Por factor común

Por triángulo cuadrado perfectos 

Por patrimonio de 2 do grado  

Diferencia de cuadrados

 la factorización es una técnica que consiste la descomposición de una expresión matemática (que puede ser un número, una suma, una matriz, un polinomio, etc) en forma de producto. Existen diferentes métodos de factorización, dependiendo de los objetos matemáticos estudiados; el objetivo es simplificar una expresión o reescribirla en términos de «bloques fundamentales», que recibe el nombre defactores, como por ejemplo un número ennúmeros primos, o un polinomio enpolinomios irreducibles.

Estadística

Concepto de estadística : se refiere ala recoleccion , análisis e interpretación de los datos obtenidos en el estudio

Población:conjunto de procedimientos destinados a recopilar,procesar y analizar la información que se obtiene  con una muestra 

Muéstral: es una parte generalmente pequeña que se toma del conjunto total para analizarla y hacer estudios 

Variable estadística : es una medida en un experimento representada por una (x) o una (y)

Variable cualitativa  : es la que manifiesta como se puede regular aceptable defectuoso feo bonito

Variable cuantitativa: es la que expresa la cantidades por ejemplo 18,9,3,75,4

Frecuencia absoluta:es el número de veces que aparece en la muestra dicho valor de la variable 

 

Frecuencia relativa : consciente entré o número de observaciones  de una clase o total de casos  de una distribución 

Frecuencia acumulativa :es la suma de las frecuencias absolutas  de los valores menores o iguales a un cierto valor de la variable 

Diagrama de sectores :es uno de los recursos estadísticos más utilizados especialmente  en los casos en que son pocos valores  

Diagrama de barras :se utiliza para representar la variable cualitativa o cuantitativa discretos en el eje horizontal  se representan sus datos  en el eje vertical 

Intervalos o clases : son rangos de clasificación que se utilizan para describir, organizar y representar los datos numéricos 

Marca de clases: es el punto medio de una clase se obtiene su mando los límites  inferiores y superiores 

Histograma : es una representación gráfica de la variable en forma de barras, donde la superficie  de cada barra proporcional  a la frecuencia de los valores representados. 

Polígonos de frecuencia : es el nombre que recibe una clase de gráfica  que se crea a partir de un histograma de frecuencia .

Medidas de dispersión : muestran la variable  de una distribución indicando por medio de un número 

Si las diferencias por medio de un número 

Rango: a la diferencia entre el valor máximo y el valor mínimo , por ello, comparte unidades con los datos .

Desviación media : es la medida de las diferencias en valor absoluto de los valores ala media. 

tabulacion y graficacion

Tabulación y Gráficas

Tabulación se refiere al hecho de calcular valores parciales para una función y compararlos en una tabla, de ahí el nombre de tabular.

Ejemplo
sea f(x)=2x

Ya hemos visto como los modelos matemáticos nos ayudan a resolver desde los problemas más simples, hasta los problemas más complejos, también hemos visto que la complejidad o simplicidad de un modelo es el producto del trabajo intelectual y el estilo de resolver las cosas según la persona que lo aborda, sin embargo, todos buscan lo mismo al final del día, resolver un problema o buscar atender una necesidad.

Para atender el tema de tabular y graficar una función pensemos en una necesidad según el siguiente caso práctico:

El profesor responsable de las actividades de Protección Civil de ha solicitado a ti y a un conjunto de tus compañeros que pintes un círculo en el centro del patio para ahí colocar el punto de encuentro que es requerido como parte del proyecto de protección civil de la escuela.

Necesitas saber dos cosas para cumplir esta asignación.

1. Conocer el diámetro del círculo en base al radio que te solicitan tenga el círculo para que sea los suficiente mente grande y de esta forma que todos lo vean.
2. Saber los metros cuadrados de área para saber la cantidad de pintura que se necesita comprar (no es lo mismo pagar un cuarto de pintura, dos litros o veinte litros).

Sabemos desde la primaria que calcular el área de un círculo se realiza mediante la siguiente fórmula:

Donde el valor de la variable “A” dependerá del valor que tenga la variable “r” que describe al radio elevado al cuadrado y multiplicado por la constante π. Y que el diámetro del círculo se calcula al multiplicar por dos el valor del radio descrito por “r”

Pongamos esta fórmula en el contexto de una función que describe el área del círculo:

Donde x al igual que en la fórmula original representará el valor del radio.

Ahora vamos a tabular los resultados, esto significa obtener el valor numérico de la función al reemplazar posibles valores de x. Esta actividad es la misma que aprendiste cuando estudiamos el valor numérico de expresiones en la Unidad 1, sección 1-7.

Vamos a emplear herramientas más modernas, usemos Excel para obtener una tabla más completa y detallada haciendo incrementos más pequeños (del orden de 0.1) y que nuestra gráfica sea más exacta. Al momento de solicitar a Excel que ponga en el plano cartesiano los valores del área que obtuvimos nos queda una gráfica del siguiente tipo:

http://www.aprendematematicas.org.mx/notas/funciones/DGB4_2_1_3.pdf

probabilidad

La probabilidad es un método mediante el cual se obtiene la frecuencia de un suceso determinado mediante la realización de un experimento aleatorio, del que se conocen todos los resultados posibles, bajo condiciones suficientemente estables. La teoría de la probabilidad se usa extensamente en áreas como la estadística, la física, la matemática, las ciencias y la filosofía para sacar conclusiones sobre la probabilidad discreta de sucesos potenciales y la mecánica subyacente discreta de sistemas complejos.

La regla de Laplace establece que:

• La probabilidad de ocurrencia de un suceso imposible es 0.
• La probabilidad de ocurrencia de un suceso seguro es 1, es decir, P(A) = 1.

Para aplicar la regla de Laplace es necesario que los experimentos den lugar a sucesos equiprobables, es decir, que todos tengan o posean la misma probabilidad.

• La probabilidad de que ocurra un suceso se calcula así:

P(A) = Nº de casos favorables / Nº de resultados posibles

Esto significa que: la probabilidad del evento A es igual al cociente del número de casos favorables (los casos dónde sucede A) sobre el total de casos posibles.

En Teoría de la probabilidad un experimento aleatorio es aquel que bajo el mismo conjunto aparente de condiciones iniciales, puede presentar resultados diferentes, es decir, no se puede predecir o reproducir el resultado exacto de cada experiencia particular. (Ej: Lanzamiento de un dado). Este tipo de fenómeno es opuesto al fenómeno determinista, en el que conocer todos los factores de un experimento nos hace predecir exactamente el resultado del mismo. Por ejemplo, conociendo la altura desde la que se arroja un móvil es posible saber exactamente el tiempo que tardará en llegar al suelo en condiciones de vacío.

En estadística, un suceso determinista es un experimento o fenómeno que da lugar a un resultado cierto o seguro, es decir, cuando partiendo de unas mismas condiciones iniciales tenemos la certeza de lo que va a suceder. La relacióncausa-efecto se conoce en su totalidad.

Por ejemplo, todos los fenómenos que siguen las leyes de la física clásica, como puede ser la caída de un cuerpo. Cuando un experimento o fenómeno no es determinista estamos ante un experimento aleatorio.

ECUACIONES

Una ecuación es una igualdad matemática entre dos expresiones algebraicas, denominadas miembros, en las que aparecen valores conocidos o datos, y desconocidos o incógnitas, relacionados mediante operaciones matemáticas.Los valores conocidos pueden ser números, coeficientes o constantes; y también variables cuya magnitud pueda ser establecida a través de las restantes ecuaciones de un sistema, o bien mediante otros procesos. Las incógnitas, representadas generalmente por letras, constituyen los valores que se pretende hallar. Por ejemplo, en la ecuación:

la variable  representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad planteada por una ecuación será cierta o falsa dependiendo de los valores numéricos que tomen las incógnitas; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que sólo ciertos valores de las variables (incógnitas) la hacen cierta.

Se llama solución de una ecuación a cualquier valor individual de dichas variables que la satisfaga. Para el caso dado, la solución es:

Uso de ecuaciones[editar · editar código]

La ciencia utiliza ecuaciones para enunciar de forma precisa leyes; estas ecuaciones expresan relaciones entre variables. Así, en física, la ecuación de la dinámica de Newton relaciona las variables fuerza F, aceleración a y masa m: F = ma. Los valores que son solución de la ecuación anterior cumplen la primera ley de la mecánica de Newton. Por ejemplo, si se considera una masa m = 1 kg y una aceleración a = 1 m/s, la única solución de la ecuación es F = 1 kg·m/s = 1 Newton, que es el único valor para la fuerza permitida por la ley.

Ejemplos:

• Ecuación de estado
• Ecuaciones de movimiento
• Ecuación constitutiva

El campo de aplicación de las ecuaciones es inmenso, y por ello hay una gran cantidad de investigadores dedicados a su estudio.

Tipos de ecuaciones[editar · editar código]

Las ecuaciones pueden clasificarse según el tipo de operaciones necesarias para definirlas y según el conjunto de números sobre el que se busca la solución. Entre los tipos más frecuentes están:

• Ecuaciones algebraicas
  • Polinómicas o polinomiales
  • De primer grado o lineales
  • De segundo grado o cuadráticas
  • Diofánticas o diofantinas
  • Exponenciales
  • Racionales, aquellas en las que uno o ambos miembros se expresan como un cociente de polinomios
• Ecuaciones trascendentes, cuando involucran funciones no polinómicas, como las trigonométricas, exponenciales, etc.
• Ecuaciones diferenciales
  • Ordinarias
  • En derivadas parciales
• Ecuaciones integrales
• Ecuaciones funcionales

Triangulos y cuadrilateros

Para triángulos:
Triángulo equilátero: (: igual: lado) tiene los tres lados iguales y también sus angulos interiores, todos iguales a 60º.
Triángulo isósceles: tienen dos lados iguales y uno desigual, lo mismo para los ángulos.
Triángulo escaleno: todos sus lados deiguales.
Triángulo rectángulo: aquel que tiene un ángulo recto, puede ser isoseles escaleno.
Triángulo acutángulo: que tiene uno de sus ángulos interiores agudo.
Triángulo obtusángulo: tiene un ángulo interior obtuso.

Dos ángulos se consideran iguales si y solo si sus lados y ángulos son iguales.
Dos ángulos son semejantes si sus ángulos son iguales pero no sus lados.

Cuadriláteros:
Paralelogramo: tiene dos lados iguales y dos desiguales, y son paralelos aquellos que tengan la misma longitud. 
Rectángulo: es un paralelogramo particular, dos lados iguales y dos desiguales, sus ángulos interiores deben medir 90º cada uno.
Cuadrado: es un rectángulo particular, todos sus lados son de la misma longitud, sus ángulos interiores son de 90º.
Rombo: es un paralelogramo particular, sus lados son todos iguales pero sus angulos interiores son iguales de a pares.
Romboide: dos lados iguales y dos desiguales, ningún lado paralelo al otro.
Trapecio: todos los lados de diferente longitud y solo dos de ellos son paralelos.

Ejemplos de tríangulos:
Una escuadra, una de las caras de una pirámide, etc.
Ejemplos de cuadriláteros:
Un barrilete, la tapa de un libro, la cara de un cubo, etc.

Un cuadrilátero es un polígono que tiene cuatro lados. Los cuadriláteros pueden tener distintas formas, pero todos ellos tienen cuatro vértices y dos diagonales, y la suma de sus ángulos internos siempre da como resultado 360º.

Por lógica todos los cuadriláteros son cuadrángulos, ya que esta definición se aplica a los polígonos de cuatro ángulos.